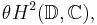Beurling–Lax theorem

In mathematics, the Beurling–Lax theorem is a theorem due to Beurling (1949) and Lax (1959) which characterizes the shift-invariant subspaces of the Hardy space 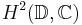$H^2(\mathbb{D},\mathbb{C})$ . It states that each such space is of the form

$\theta H^2(\mathbb{D},\mathbb{C}),$

for some inner function $\theta$ .

References

Ball, J. A. (2001), "Beurling–Lax theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=b/b120200
Beurling, A. (1949), "On two problems concerning linear transformations in Hilbert space", Acta Math. 81: 239–255, doi:10.1007/BF02395019, MR 0027954
Lax, P.D. (1959), "Translation invariant spaces", Acta Math. 101 (3-4): 163–178, doi:10.1007/BF02559553, MR 0105620
Jonathan R. Partington, Linear Operators and Linear Systems, An Analytical Approach to Control Theory, (2004) London Mathematical Society Student Texts 60, Cambridge University Press.
Marvin Rosenblum and James Rovnyak, Hardy Classes and Operator Theory, (1985) Oxford University Press.